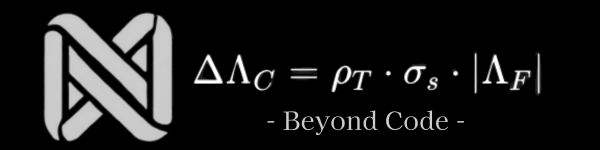This work introduces a fundamentally new theoretical and computational framework—the Λ³ (Lambda-cubed) theory—to address the Yang-Mills mass gap problem, one of the deepest unsolved questions in modern physics. Departing from conventional descriptions based on time evolution and energy spectra, Λ³ theory recasts all physical phenomena as topological pulsations (irreversible jumps) of a structural tensor field Λ.

In this study, the author provides both theoretical arguments and direct numerical simulations for SU(2) and SU(3) lattice Yang-Mills models, demonstrating that the mass gap is not merely a minimal quantum of energy, but a structural necessity: it emerges as the minimal nonzero “pulsation” (ΔΛ_C > 0) required to cross topological barriers in state space. The simulations explicitly show that any excitation from the vacuum demands a finite structural jump, thereby providing clear numerical evidence for the mass gap as a geometric/topological phenomenon.

The Λ³ framework further redefines mass as “topological inertia”—the minimal structural cost for maintaining topological stability—and interprets the vacuum not as an empty ground state, but as a dynamic, nontrivial manifold of minimal tension density, rich in structural and topological order. These innovations not only resolve foundational issues associated with “unprovability” in the mass gap problem but also unify the description of phase transitions, latent heat, and other non-perturbative phenomena across different scales.

The results suggest a paradigm shift in the axiomatic foundations of physics, paving the way for unified structural descriptions of matter, phase transitions, and even computation. All code and data necessary to reproduce the simulations are provided.